MCL
Introduction
蒙特卡洛定位算法(Monte Carlo Localization, MCL)的公式推导涉及粒子滤波(Particle Filter)的数学基础。粒子滤波是一种基于递归贝叶斯估计的方法,用于对系统状态进行估计。其基本目标是根据传感器观测和运动模型来估计机器人的位置和姿态。
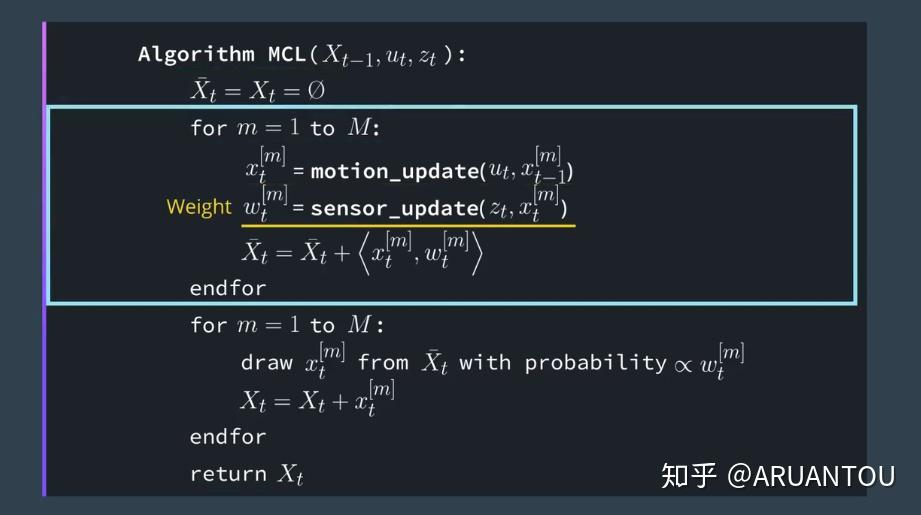
Algorithm

第一步:随机生成M个粒子(这些粒子都是有算计的方向和位置)
第二步:根据小车的运动参数(里程计,速度等)来估算每一个粒子基于 的 的预测位置。这里的预测与KF的算法相同。
第三步:根据传感器的测量数据,计算出每一个粒子的权重。(权重计算方式有很多,简单的理解可以认为是和真实传感器测量值之间的差别大小,比如说当前的一个例子的预测位置和测量目标之前的距离和 差别大, 越大权重越小,小的权重说明距离真实的位置)。随后更新每一个粒子的状态。
第四步:重采样,从所有粒子中根据新的权重值获取M个粒子。
之后不断重复上面的4步来实现定位的效果。
初始化
在状态空间中随机生成一组粒子。每个粒子代表一个可能的机器人位置和姿态。初始粒子的分布可以是均匀的,也可以根据先验信息进行初始化。
- 粒子的的定义:
$$ \xi_t^{(i)} = ({x}_t^{(i)}, w_t^{(i)}) $$
class Particle:
def __init__(self, init_pose, weight):
self.pose = init_pose
self.weight = weight
- 信念分布近似
$$ P(x_t^* \in X) = \int_{{x} \in X} b_t({x}) d{x} \approx \sum_{i=0}^{N-1} w_t^{(i)} \delta({x}_t^{(i)} \in X) $$
- 权重计算
$$ L_j(x | {z}_j) = \mathcal{N}\left[ {z} = {z}_j | {h}_j({x}), Q_j({x}) \right] $$
multivariate_normal(mean=particle_suggest_pos, cov=cov).pdf(obs_pos)
$$ Q_j(x) = \begin{pmatrix} [\ell_j({x})\sigma_\ell]^2 & 0 \ 0 & \sigma^2_\varphi \end{pmatrix} $$
$$ w_t^{(i)} = L_j (x_t^{(i)} | {z}_{j,t} ) \hat{w}_t^{(i)} $$
$$ w_t^{(i)} = L_j (x_t^{(i)} | {z}_{j,t} ) \hat{w}_t^{(i)} $$
$\ell_j({x})$: x到landmark的距离
$h_j$ :观测函数
distance_dev = distance_dev_rate*particle_suggest_pos[0]
cov = np.diag(np.array([distance_dev**2, direction_dev**2]))
self.weight *= multivariate_normal(mean=particle_suggest_pos, cov=cov).pdf(obs_pos)
Example code:
class Particle:
def __init__(self, init_pose, weight):
self.pose = init_pose
self.weight = weight
def motion_update(self, nu, omega, time, noise_rate_pdf):
ns = noise_rate_pdf.rvs()
pnu = nu + ns[0]*math.sqrt(abs(nu)/time) + ns[1]*math.sqrt(abs(omega)/time)
pomega = omega + ns[2]*math.sqrt(abs(nu)/time) + ns[3]*math.sqrt(abs(omega)/time)
self.pose = IdealRobot.state_transition(pnu, pomega, time, self.pose)
def observation_update(self, observation, envmap, distance_dev_rate, direction_dev): #変更_
for d in observation:
obs_pos = d[0]
obs_id = d[1]
##パーティクルの位置と地図からランドマークの距離と方角を算出##
pos_on_map = envmap.landmarks[obs_id].pos
particle_suggest_pos = IdealCamera.observation_function(self.pose, pos_on_map)
##尤度の計算##
distance_dev = distance_dev_rate*particle_suggest_pos[0]
cov = np.diag(np.array([distance_dev**2, direction_dev**2]))
self.weight *= multivariate_normal(mean=particle_suggest_pos, cov=cov).pdf(obs_pos)
class IdealCamera:
def __init__(self, env_map, distance_range=(0.5, 6.0),
direction_range=(-math.pi/3, math.pi/3)):
self.map = env_map
self.lastdata = []
self.distance_range = distance_range
self.direction_range = direction_range
def visible(self, polarpos): # ランドマークが計測できる条件
if polarpos is None:
return False
return self.distance_range[0] <= polarpos[0] <= self.distance_range[1] and self.direction_range[0] <= polarpos[1] <= self.direction_range[1]
def data(self, cam_pose):
observed = []
for lm in self.map.landmarks:
z = self.observation_function(cam_pose, lm.pos)
if self.visible(z): # 条件を追加
observed.append((z, lm.id)) # インデント
self.lastdata = observed
return observed
@classmethod
def observation_function(cls, cam_pose, obj_pos):
diff = obj_pos - cam_pose[0:2]
phi = math.atan2(diff[1], diff[0]) - cam_pose[2]
while phi >= np.pi: phi -= 2*np.pi
while phi < -np.pi: phi += 2*np.pi
return np.array( [np.hypot(*diff), phi ] ).T
预测
更新
重采样
重采样是为了避免粒子权重的退化问题,使高权重的粒子被复制,而低权重的粒子被丢弃。这一步骤有助于集中粒子在可能的状态区域。
状态估计
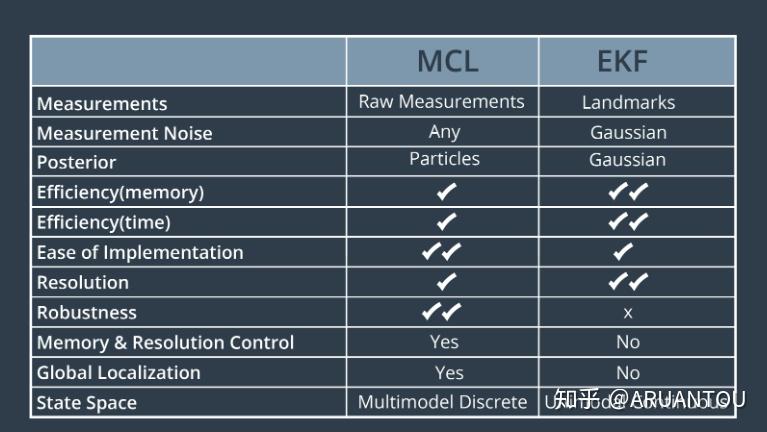
MCL VS EKF